2933: 05-07-C01-三角形的面积(1)(L3)

# 05-07-C01-三角形的面积(1)(L3) ## 题目背景 对一个直角三角形，如果已知两条直角边的长度为a和b，可以很容易求出这个直角三角形的面积为：a*b/2。但是普通的三角形，怎么求它的面积呢？也就是要考虑以下问题。 已知三角形的3条边的边长a、b、c（假定可以构成三角形），求这个三角形的面积。 上述问题可以用海伦公式（或称为海伦－秦九韶公式）求解。古希腊的数学发展到亚历山大里亚时期，数学的应用得到了很大的发展，其突出的一点就是三角术的发展，在解三角形的过程中，其中一个比较难的问题是如何利用三角形的三边直接求出三角形面积。 这个公式是由古希腊数学家阿基米德得出的，但人们常常以古希腊的数学家海伦命名这个公式，称此公式为海伦公式，因为这个公式最早出现在海伦的著作《测地术》中，并在海伦的著作《测量仪器》和《度量数》中给出证明。 中国宋代的数学家秦九韶在1247年独立提出了“三斜求积术”，虽然它与海伦公式形式上有所不同，但它完全与海伦公式等价，它填补了中国数学史中的一个空白，从中可以看出中国古代已经具有很高的数学水平。

 ## 题目描述 从键盘上输入三角形的3条边的边长a、b、c（假定输入的3条边长可以构成三角形），根据公式 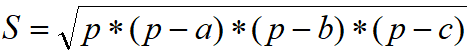， 其中p=(a+b+c)/2，求三角形的面积。 

3.4 6.5 5.5

9.35