3640: 色球(第四轮02)
题目描述
牛牛有n种颜色的彩色小球(编号 1 到n), 每种颜色的小球他都有无限多个。他 还有n个球桶(编号 1 到n), 球桶的内径与小球直径相当且高度是无限大的, 因 此能容纳无限多的小球。他想用这些小球和球桶玩游戏。
一开始这些球桶都是空的, 紧接着他会顺次地做m个操作, 每个操作都是以下 3 类操作中的一个。
1. 把x个颜色为y的彩色小球放到第Z个桶的最上面(pusℎ xy Z);
2. 把最上面的x个小球从第 z 个桶内拿出来(pop x Z);
3. 把第u个桶的所有小球依次从顶部拿出放入第v个桶内(put uv) 。
现在他已经确定好了这m个操作,但在他开始玩之前,他想知道每次他进行第二 类操作取出的最后一个小球是什么颜色。
输入
第 1 行两个正整数n, m。
接下来m行每行是一个操作,
如果为第一类操作,则格式为pusℎ xy Z(x, y, Z为正整数,1 ≤ x ≤ 1e9, 1 ≤ y, Z ≤ n);
如果为第二类操作,则格式为popx Z(x, Z为正整数,1 ≤ x ≤ 1e9, 1 ≤ Z ≤ n)保 证第Z个桶内至少有x个小球;
如果为第三类操作,则格式为put uv(u, v为正整数, 1 ≤ u, v ≤ n, u ≠ v)
输出
对于每个第二类操作,输出牛牛取出的最后一个小球的颜色编号。
样例输入 复制
2 5
push 1 1 1 push 1 2 1 push 2 3 2 put 1 2
pop 2 2样例输出 复制
2提示
【样例 1 输入】
2 5
push 1 1 1 push 1 2 1 push 2 3 2 put 1 2
pop 2 2
【样例 1 输出】
2
【样例 1 说明】
5 个操作后的情况依次如下:
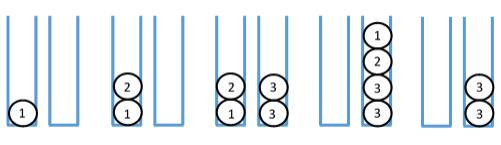
【数据范围】
对于 30%的数据,满足1 ≤ n, m ≤ 1000
对于另外 10%的数据, 所有第一类操作满足x = 1 对于另外 10%的数据, 所有第二类操作满足x = 1 对于 100%的数据,满足1 ≤ n, m ≤ 200000