3653: 路径难题(第六轮03)
题目描述
牛牛最近在为自己的出行烦忧。
牛牛所在的城市可以简化为 n 个点,编号从 1 开始。由 m 条无向边表达两两之 间的路径。第 i 条边连通点ui 和vi,距离为di 。
牛牛是个懒人,他宁愿叫出租车也不愿意走路。牛牛所在城市的出租车不计算起 步价, 直接按照距离计费, 每 r 单位距离 1 元, 向上取整, 即如果单次行进了 p
 元。如果多次乘坐分开收费。
元。如果多次乘坐分开收费。
牛牛所在的城市还有 k 路不同的公交车,每一路公交车都是双向的,有ti 个站台, 可以正着坐,也可以反着坐,但每路公交车仅会在规定的站台停车。牛牛从任意 一个位置上车,可以从该路公交车的任意站台下车,仅需付一份该路的公交车车 费ci 元。但坐到终点站之后必须下车。
牛牛有 q 个规划,其中第 i 个规划为从ai 位置移动到bi 位置,牛牛想知道这样的 移动最小需要的花费是多少。花费是指出租车的花费和公交车的花费之和。
输入
第一行输入五个整数 n,m,k,r,q,分别表示牛牛所在的城市的点数,边数,公交车 有多少路,出租车收费标准和规划次数。
第二行起 m 行,第 i 行三个整数ui,vi, di,表示对应的边连接ui 和vi,距离为di 。 随后 k 行,每行第一个整数ti 表示对应路公交车的站台数目。第二个整数ci 表示 该路公交车的收费。随后ti 个整数,分别表示该路公交车停的站台。
随后 q 行,第 i 行两个整数ai, bi 表示牛牛计划从ai 到bi,想知道其最小花费。
输出
输出 q 行,每行一个整数ansi,表示第 i 个规划的答案。
样例输入 复制
5 6 1 10 5
1 2 15
2 3 177
3 5 73
4 2 37
1 5 66
1 4 43
3 11 1 3 5
1 2
1 4
1 3
4 5
2 3样例输出 复制
2
5
11
11
13提示
【样例 1 解释】
1 到 2 直接打车,花费 15/10 向上取整,花费为 2。
1 到 4 直接打车,花费 43/10 向上取整,花费为 5。
1 到 3 直接坐公交车, 花费为 11。
4 到 5 直接打车,从 4 到 1 到 5,花费 109/10 向上取整,花费为 11。
2 到 3 先打车到 1,花费 2,再坐公交车到 3,花费 11,共计花费 13。
【数据范围】
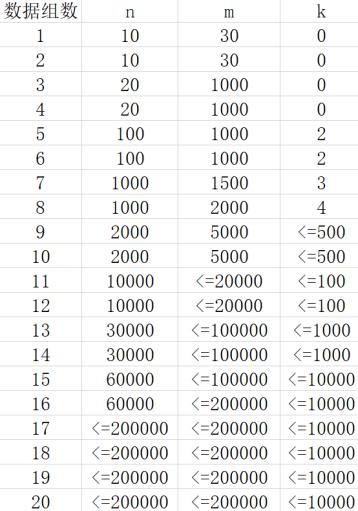
对于100%的数据有2 ≤ n ≤ m + 1 ≤ 2 ⋅ 105,0 ≤ k ≤ 10000, 1 ≤ q ≤ 10,2 ≤ ti ≤ n, ∑ ti ≤ 400000, 1 ≤ ai, bi, ui, vi ≤ n, 1 ≤ di, r ≤ 106,1 ≤ ci ≤ 109
数据保证 n 个点 m 条边的图是一张连通图。但数据并不保证没有重边和自环。