3679: 牛表(第一轮01)
题目描述
给出三个整数x, y, P(1 ≤ x, y < P), P 为素数,可以重复对x执行如下操作: 选择一个整数z ∈ [1, P − 1],花费∣ x − z ∣的牛币,使得x = x ∗ zmod P 。 最小需要花费多少牛币才能使得x = y?
设 ans(i, j) 为 当 x = i, y = j 时 的 答 案 , 为 了 减 少 输 出 , 你 需 要 输 出
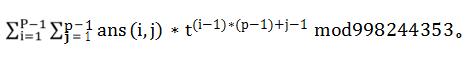
输入
输入一行两个整数P, t。
输出
样例输入 复制
2 1样例输出 复制
0提示
【样例 1 输入】
2 1
【样例 1 输出】
0
【样例 1 说明】
ans矩阵为: 0
答案为: 0 ∗ 10^0 = 0
【样例 2 输入】
3 233
【样例 2 输出】
233
【样例 2 说明】
ans 矩阵为: 0,1
0,0
答案为0 * 233^0 + 1 * 233^1 + 0 * 233^2 + 0 * 233^3 = 233
【样例 3 输入】
5 233
【样例 3 输出】
889807030
【样例 3 说明】
ans 矩阵为: 0,1,2,1
0,0,2,0 0,1,0,0 0,1,2,0
答案为: 0 * 233^0 + 1 * 233^1 + 2 * 233^2 + 1 * 233^3 + 0 * 233^4 + 0 * 233^5 + 2 * 233^6 + 0 * 233^7 + … …
【样例 4 输入】
1999 2333
【样例 4 输出】
982345126
【数据范围】