3692: 空间跳跃(第四轮02)
题目描述
牛妹在无穷多个平行宇宙中跳跃,每个宇宙都有一个整数编号,且对于每个整数 n ∈ Z,都有唯一一个宇宙的编号是n。
牛妹掌握了三种空间跳跃技术,分别是:
1. 如果当前在编号为n的宇宙, 且min(|n |, |n − d|) ≤ l, 则她可以跳跃到编号为 n − d的宇宙,其中d 和 l都是给定的正整数。
2. 如果当前在编号为n的宇宙,则她可以跳跃到编号为2n 的宇宙;
3. 如果当前在编号为n的宇宙,且n ≡ 1(mod3),(即 n =. . . , −5, −2,1,4, . .. 时)则
她可以跳跃到编号为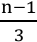 的宇宙;
的宇宙;
牛妹一开始在编号为1的宇宙中, 她可以随意的使用这三种空间跳跃技术在宇宙 中跳跃。她有q 个想去的目的地n1, n2, . . . , nq,她想知道对于每个i (1 ≤ i ≤ q),她 需要怎么从编号为1的宇宙跳跃到编号为ni 的宇宙。由于每次跳跃需要巨大的能 量,所以每次牛妹只能跳跃不超过1500 次。
输入
第一行三个整数q, d, l,以空格分离。
接下来q行,第i 行一个整数 ni,表示目的地宇宙的编号。
输出
输出q行,第i行输出ki oi,0 oi, 1 . . . oi,ki
其中oi,0 = 1, oi,ki = ni,且可以通过三种空间跳跃技术之一从编号为oi,j 的宇宙跳 跃到编号为 oi,j+1的宇宙 (0 ≤ j < ki)。
输出需要满足对于任意的1 ≤ i ≤ q和0 ≤ j ≤ ki,0 ≤ ki ≤ 15000且-10^18 ≤ oi,j ≤10^18 。
输出任意一组满足上述所有条件的解即可,数据保证至少存在一组满足上述所有 条件的解。
样例输入 复制
5 3 10000
10
-9
0
-7
1样例输出 复制
6 1 2 4 8 16 5 10
13 1 -2 -5 -10 -20 -7 -14 -28 -56 -19 -38 -13 -26 -9
8 1 2 4 8 16 5 10 3 0
5 1 -2 -5 -10 -20 -7
0 1
提示
【样例 1 输入】
5 3 10000
10
-9
0
-7
1
【样例 1 输出】
6 1 2 4 8 16 5 10
13 1 -2 -5 -10 -20 -7 -14 -28 -56 -19 -38 -13 -26 -9
8 1 2 4 8 16 5 10 3 0
5 1 -2 -5 -10 -20 -7
0 1
【数据范围】
对于 10%的数据,满足∣ ni ∣≤ 103, d = 1, l = 1500。
对于 30%的数据,满足∣ ni ∣≤ 10^3 。
对于另外 10%的数据,满足∣ ni ∣≤ 10^6, l = 10^6 。
对于另外 20%的数据,满足∣ ni ∣≤ 10^6 。
对于 100%的数据,满足∣ ni ∣≤ 10^7, 1 ≤ q ≤ 20,1 ≤ d ≤ 10^6, 10^3 ≤ l ≤ 10^6 。