3702: 跑步路线(第六轮04)
题目描述
牛牛最近开始晨跑了,他把城市的路线抽象成了一张无向图,每个路口视为一个 点,路口之间的路视为一条边。
牛牛估计了跑过每条边的所需时间,为了保守估计所需时间,牛牛认为经过每一 个点也需要t0 的时间。
比如对于路线 1->3->2->4,其中3和2各经过了一遍,需要花费2 ∗ t0 的时间。
在经过很多次糟糕的路线体验之后,牛牛决定请你来帮他设计一条路线,他的要 求是:
1. 需要按顺序经过 k个点,用a1, a2, ⋯ , ak 表示,这些点可能重复。偶尔可能会有 相邻的点相同的情况,这种情况下不需要额外计算t0 的花费。
2. 牛牛希望经过的路线在地图的最小生成树上。
3. 在满足以上两条的需求下,使总距离尽可能短。
牛牛起点在位置a1,牛牛想知道这样的路线中,最短的路线的距离是多少 。
输入
第一行输入两个整数n, m,表示路口的数目和边的个数。
随后m行,每行输出两个整数u, v, w,表示有一条边连接u和v,需要花费的时间是w。
随后一行两个整数k, t0, 分别表示需要经过的k个点和经过每一个点的时间t0 。 随后一行k个数字,表示牛牛需要按顺序经过的k个点。
输出
样例输入 复制
5 7
1 2 6
2 3 7
3 4 8
4 5 25
5 1 20
2 5 17
2 4 12
6 100
1 2 3 4 5 1样例输出 复制
776提示
【样例 1 输入】
5 7
1 2 6
2 3 7
3 4 8
4 5 25
5 1 20
2 5 17
2 4 12
6 100
1 2 3 4 5 1
【样例 1 输出】
776
【样例 1 说明】
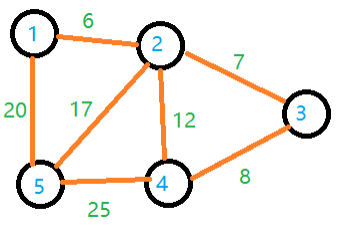
先计算边的总花费时间: 1->2 = 6
2->3 = 7
3->4 = 8
4->5 = 7+8+17 = 32
5->1 = 17+6 = 23
边的花费共计为 76 。
再计算路口的总花费时间,路线是:
1->2->3->4->3->2->5->2->1, 共花费 7*100 的时间。
共计花费 776。
【样例 2 输入】
5 7
1 2 6
2 3 7
3 4 8
4 5 25
5 1 20
2 5 17
2 4 12
9 100
1 1 2 2 3 4 5 1 1
【样例 2 输出】
776
【样例 2 说明】
样例 2 用于解释题目出现的相邻点相同情况,应当忽略之后出现的相同点,图与 样例 1 一致。
对于 60% 的数据有 n, m, k ≤ 100000。
至少有 50% 的数据是随机构造的。
对于总量 40% 的数据 t0 = 0 。
对 于 100% 的 数 据 有 1 ≤ n, m ≤ 2 ⋅ 105, 1 ≤ k ≤ 106, 1 ≤ t0, w ≤ 109, 1 ≤u, v ≤ n。
数据保证不会有两条距离相同的边,且保证图连通。
CD 的大数据下载链接:
链接: https://pan.baidu.com/s/1zupTECKeGEpNM-9tQ4TzlQ 提取码: NOIP