3726: 嘤嘤的珂朵莉树(第四轮04)
题目描述
现在,嘤嘤有一棵含有 n 个结点且根为 1 号结点的树,嘤嘤将其命名为珂朵莉 树,每个结点具有一个权值,每个结点与根的距离就是该结点的深度。
然后,嘤嘤会在这棵树上增加 m 条辅边,任意一条辅边不会和原来的树边或其 他辅边重合(增加的辅边不会影响结点的深度)。
之后,嘤嘤会进行进行 q 次操作。
操作一:让结点 u 的权值增加 k , 并对与结点 u 相邻的结点中, 深度比结点 u 小的结点重复操作一。
操作二:让结点 u 的权值增加 k , 并对与结点 u 相邻的结点中, 深度比结点 u 大的结点重复操作二。
嘤嘤想知道,经过 q 次操作后,所有结点的权值分别是多少。
输入
第一行三个整数n, m, q , 分别表示树的结点个数,辅边条数,操作次数。
第二行 n 个整数 ai,表示每个结点的初始权值。
接下来 n − 1 行,每行两个整数 u, v (1 ≤ u, v ≤ n, u ≠ v) 表示树的结构。
接下来 m 行,每行两个整数 u, v (1 ≤ u, v ≤ n, u ≠ v) 表示辅边连接的两个结 点。
接下来 q 行,每行三个整数 t(1 ≤ t ≤ 2), u (1 ≤ u ≤ n), k ,分别表示操作类型, 操作的结点。
输出
一行 n 个整数,表示树上每个结点的权值,由于权值可能很大,请将权值对 109 + 7进行取模。
样例输入 复制
7 2 4
1 1 1 1 1 1 1
1 2
1 3
2 4
2 5
3 6
3 7
4 3
7 1
2 1 1
1 4 1
1 7 1
2 5 1样例输出 复制
6 3 4 4 3 2 4提示
【样例 1 输入】
7 2 4
1 1 1 1 1 1 1
1 2
1 3
2 4
2 5
3 6
3 7
4 3
7 1
2 1 1
1 4 1
1 7 1
2 5 1
【样例 1 输出】
6 3 4 4 3 2 4
【样例 1 说明】
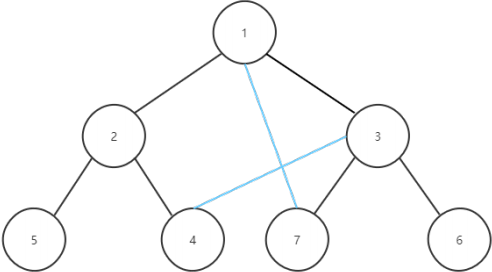
图中蓝色的边即为辅边。
【样例 2 输入】
6 5 3
0 0 0 0 0 0
1 2
2 3
3 4
1 5
5 6
1 3
5 3
1 6
2 6
5 4
2 1 1
2 3 1
2 6 1
【样例 2 输出】
1 1 4 5 1 4
【数据范围】
对于 20%的数据 n ≤ 1000, m = 0, q ≤ 1000, k ≤ 1000。
对于另外 20% 的数据 n ≤ 10 5, m = 0 ,保证没有操作一。
对于 100%的数据 n ≤ 10^5 , m ≤ 2 × 10^5, q ≤ 2 × 10^5, k ≤ 109 。