3732: 几何(第六轮02)
题目描述
相信平面几何对你来说一定不陌生。现在, 请你拿出纸和笔来,尝试解决这样一 道几何题。
给定一个整数。, 在第一象限内画出所有端点分别在两个坐标轴上, 且端点横纵 坐标和为。的所有线段, 请你尝试计算出这些线段与坐标轴围成的图形中包含的 三角形个数。
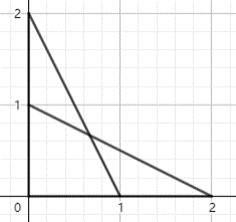
例如, 当。为3时,你将画出(0, 2)(1, 0)与(0, 1)(2, 0)两条线段,这些线段与坐标 轴围成的 图形如图 所示。图 中共有 4 个三角形, 其顶点坐 标分别为
(0, 2)(0, 0)(1, 0)、(0, 2)(0, 1)(2/3, 2/3)、(1, 0)(0, 0)(2, 0)、(2/3, 2/ 3)(1, 0)(2, 0)。
输入
共一行,为一个整数。,含义如题目描述所述。
输出
共一行,表示你所求解的三角形数量。
由于这个数量可能会很大,你只需要输出数量对998244353取模后的值。
样例输入 复制
2样例输出 复制
1提示
【样例 1 输入】
2
【样例 1 输出】
1
【样例 2 输入】
3
【样例 2 输出】
4
【样例 2 说明】
样例解释请见问题描述部分。
【样例 3 输入】
4
【样例 3 输出】
10
【样例 3 说明】
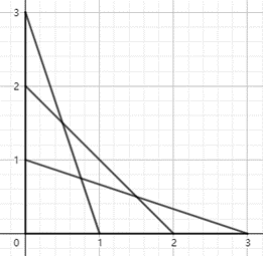
【样例 4 输入】
5
【样例 4 输出】
20
【样例 5 输入】
996
【样例 5 输出】
164674490
【样例 6 输入】
999996
【样例 6 输出】
608861885
【样例 7 输入】
999999996
【样例 7 输出】
536236838
【数据范围】
对于10%的数据:g ≤ 5。
对于20%的数据:g ≤ 10 。
对于40%的数据:g ≤ 10^3 。
对于70%的数据:g ≤ 10^6 。
对于100%的数据: 2 ≤ g ≤ 10^9 。
可能会用到的公式: (n + 1)3 − n3 = 3n2 + 3n + 1