3742: 神奇的变换(第二轮04)
题目描述
有一天,玥玥在电视上,看到了一种神奇的数字变换。
这种变换是这样的:
首先我们拿到一个正整数,然后对它分别进行以下分解:
1. 分解它的质因数, 数一数其质因数的指数,如果有一个质因数的指数 ≥ 2 , 写下 0;否则,若有奇数个质因数,写下 −1 ,否则写下 1。
2. 分解其所有正约数,写下其约数个数以及约数总和。
显然,对于每一个数 x,经过变换后将得到 3 个整数。
玥玥试了试,发现他算出了正确的答案,他太开心了!
然而,很不幸,这一切被玥玥的老师看见了。老师总算是找到了给玥玥出题的机 会,于是在第二天,老师给玥玥留了一道《好》题。
老师给玥玥了 n 个正整数,排成一排。老师让玥玥仔细看看这个序列(名字叫 a),然后告诉了玥玥他会问 q 个问题。每一个问题中,老师给出两个数 l, r,让
玥玥算出数字 x 的答案,其中x = Πi(r)=l ai 。
“老师,这个数(指 x)太大了怎么办?”
“没关系, 你只需要告诉我答案对 109 + 7 取模的结果就行了(完全理解成了答 案太大)。实在不行的话,可以请别人帮忙哦。 ”
这下可把玥玥难住了。她请班上 OI 最强的你来帮他解决这个问题,毕竟,这可 能会给她加不少德育分啊!
老师比较善良,所以每一次回答问题时,只需要回答答案中的第 type 问就可以 ( 1 ≤ type ≤ 3)。注意,这里的输出 x 的答案指的是输出 x 经过上述变换得 到的 3 个整数中的第 type 个。
由于老师的问题是一个一个问的,所以本题强制在线。
输入
第一行三个整数 n, q, type ,其中 type 表示询问种类。
第二行 n 个整数,第 i 个整数代表 ai 。
后面 q 行每行两个整数 l′, r′,表示一个询问。
设 last 为上次询问的答案,初始为 0。则询问的区间为 [l = l ′xor last, r =r ′xor last],保证 1 ≤ l ≤ r ≤ n 。
你需要对该区间回答第 type 种询问。
输出
样例输入 复制
5 3 1
1 2 3 4 5
2 4
3 5
1 3样例输出 复制
0
0
1提示
【样例 1 输入】
5 3 1
1 2 3 4 5
2 4
3 5
1 3
【样例 1 输出】
0
0
1
【样例 1 说明】
样例询问的区间为[2,4],[3,5],[1,3],由于 type 为 1, 所以回答的是区间乘积的素 因子分解的特点(1 、0 、-1)
【样例 2 输入】
5 3 2
1 2 3 4 5
2 4
11 13
13 15
【样例 2 输出】
8
12
4
【样例 2 说明】
样例询问的区间为[2,4],[3,5],[1,3],由于 type 为 2,所以回答的是区间乘积的因 子数量。
当得到第一问的结果为 8 时,第二次询问 11,13,我们可以通过 11 异或 8 得 到 3,13 异或 8 得到 5。这样就可以知道第二次询问的区间是 [3,5] 了,算出 结果 12 之后,再去用 12 和第三次询问进行异或,得到第三次询问的内容 [1,3]
【样例 3 输入】
5 3 3
1 2 3 4 5
2 4
63 57
169 171
【样例 3 输出】
60
168
12
【样例 3 说明】
样例询问的区间为[2,4], [3,5], [1,3],由于 type 为 3,输出的是因子和
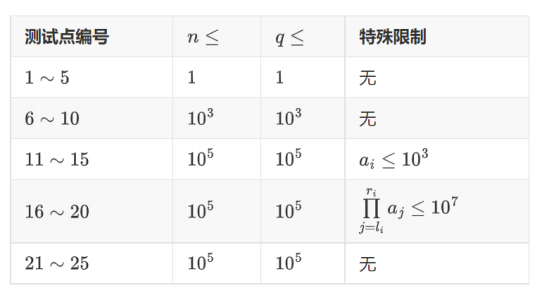
【数据范围】
1 ≤ n, q ≤ 10^5 1 ≤ a i ≤ 10^8 1 ≤ type ≤ 3
对于所有编号模 5 余 1 的测试点, type = 1。
对于所有编号模 5 余 2,3 的测试点, type = 2。
对于所有编号模 5 余 4,0 的测试点, type = 3。