3751: 喷泉(第五轮01)
题目描述
鸡尾酒喜欢打保龄球,他觉得打了保龄球就可以确保爆零。但是 OIer 不打保龄 球,鸡尾酒想了一个办法—— OIer 都不会几何,那就搞一道几何 T1 帮助大家 爆零。
鸡尾酒道白浅妹妹家的路是一条线段。在这条路的旁边有一个圆形的喷泉,它喷 出的水晶莹透明, 美丽~~动人~~。于是, 它就引来了一条小狗, 天天围着喷泉 转。
白浅妹妹很喜欢这条狗,天天都在路上距离最近的点看小狗,而小狗也很喜欢她, 也在最近的地方看她。
而鸡尾酒不喜欢,每次都要躲在路上最远的地方,而小狗就在最远的地方躲鸡尾 酒。
请问, 白浅妹妹看小狗时,和鸡尾酒躲狗的时候,他们与狗的欧几里得距离分别 是多少?(欧几里德距离即直线距离,由两点的横坐标之差的平方加纵坐标之差 的平方求和再开根号获得,即勾股定理)
另外一提,为了简化题意,路上总有一个点使得它到喷泉的连线垂直于路。鸡尾 酒和白浅妹妹不会同时出现在这条路上。
输入
第一行一个正整数 t 表示数据组数。
接下来 t 行,每行七个正整数 x1, y1, x2, y2, x3, y3, r ,表示鸡尾酒家的坐标、白 浅妹妹家的坐标、喷泉圆心的坐标及半径。
输出
对于每组数据,输出一行两个两位实数,表示白浅妹妹与狗的距离和鸡尾酒与狗 的距离。注意: 本题输出量较大,请尽量选择较快速的输出方式(例如 printf)
样例输入 复制
4
1 1 1 4 4 4 0
11 1 1 4 9 8 0
11 4 1 4 9 8 1
91665 81788 66905 42038 75347 76904 2844样例输出 复制
3.00 4.24
6.13 8.94
3.00 9.94
8424.51 38717.46提示
【样例 1 说明】
三 张 图 分 别 对 应 样 例 1 的 前 三 组 数 据 。
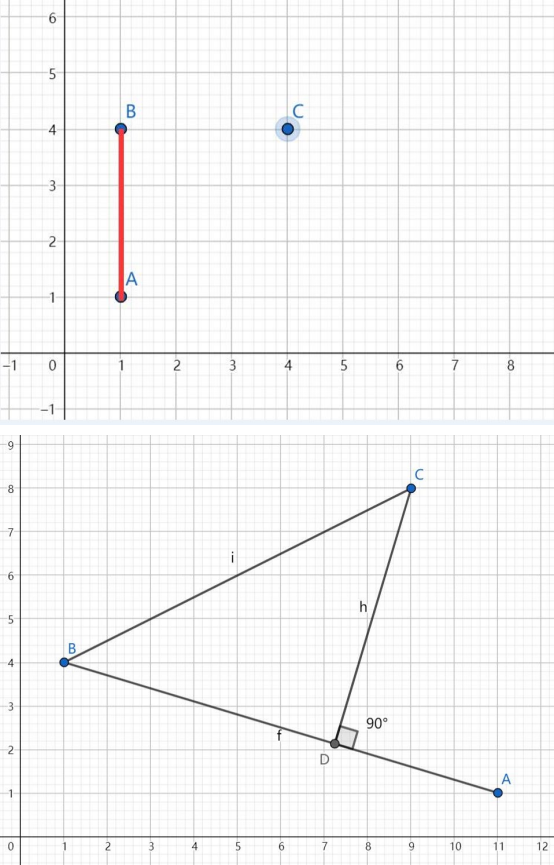
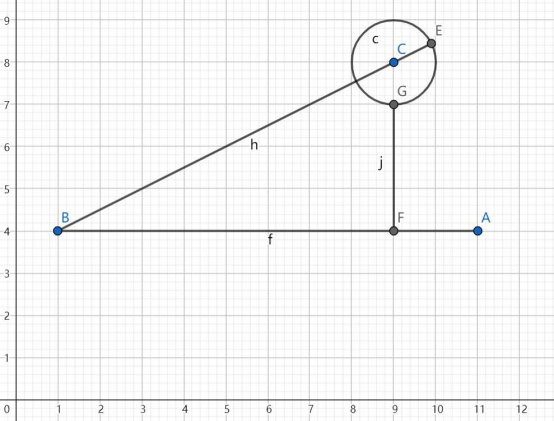
【数据范围】
对于所有数据, 1 ≤ t ≤ 10 5, 0 ≤ xi , yi , r ≤ 105, (x1, y1 ) ≠ (x2, y2)。
保证题面中所提到的垂直条件, 并且路上不存在点使得其在喷泉的边缘或内部。
