3753: 子集(第五轮03)
题目描述
清楚姐姐有一个正整数 M。对于集合 S,她定义 F0 (S) = [∑X∈S X = M]
以及
Fk (S) = ∑ T⊆SFk−1 (T)(k > 0)
给定集合 S = {a1 , a2 , ⋯ , an } 与非负整数 k,你需要求出 Fk (S) 对 10 9 + 7
取模的值。 其中:
[condition] 表示当 condition 为真时值为 1,否则为 0。
特别地,我们认为空集内所有元素和为 0; ∅ ⊆ ∅。
你可以通过样例 1 的第二组数据来更好地理解第二点。
输入
本题有多组数据。第一行一个正整数 T 表示数据组数;对于每组数据: 第一行三个正整数 n, M, k 。
第二行 n 个正整数 a1 , a2 , ⋯ , an 。
输出
输出一行一个正整数表示Fk (S) 对 10^ 9 + 7取模的值。
样例输入 复制
3
3 5 2
2 5 3
6 0 2
1 1 4 5 1 4
7 10 3
1 9 1 9 8 1 0样例输出 复制
6
64
2268提示
样例 1 说明】
对于第一组数据:
对于 k = 0, F0 ({2,3}) = F0 ({5}) = 1,其余的都是 0。 对于 k = 1:
F1 ({2,3}) = F1 ({5}) = F1 ({2,5}) = F1 ({3,5}) = 1; F1 ({2,5,3}) = 2;
其余的都是 0。
因此, F1 ({2,3,5}) = 1 + 1 + 1 + 1 + 2 = 6;
对于第二组数据:由于 M = 0 且任意 ai ≠ 0 ,因此只有 F0 (∅) = 1,其余的 都是 0。
因此,对于任意集合 T 均有 F1 (T) = 1 ,从而 F2 (S) = ∑ T⊆SF1 (T) = 2 ∣S∣ = 64。 注意,由于我们认为 ∅ ⊆ ∅,因此同样有 F1 (∅) = F0 (∅) = 1。
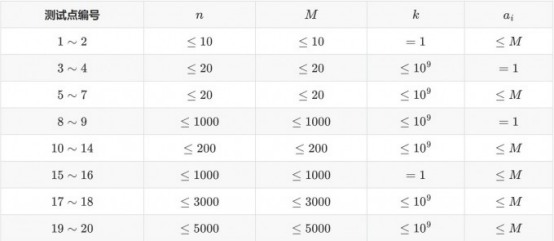
【数据范围】
对于 100% 的数据,1 ≤ T ≤ 5,0 ≤ ai ≤ M ≤ 5000,1 ≤ n ≤ 5000,0 ≤ k ≤ 10^9 。