3798: 打标签(第四轮04)
题目描述
白浅妹妹的班里有许多同学。
白浅妹妹是一个爱打标签的孩子, 在她的眼里, 每一个人有 n 种属性, 每个人的每个属性 都是一个 [0, k] 中的整数。
显然,在白浅妹妹这种打标签的方法下,所有人恰好被分为了 (k + 1)n 类。 巧合的是,白浅妹妹的班级里,每一类人恰好有一个。
白浅妹妹认为,班级里的两个人可以交朋友,当且仅当这两个人每一个属性,差的绝对值都 不超过 1 。当然,每一个人都可以和自己交朋友。
此外,白浅妹妹认为,班级里面的每一个同学都有一个友好度(可以是负数)。
她认为,一个人在这个班级里的存在感,和她朋友的友好度是有关的。所以白浅妹妹定义一 个人的存在感,为这个人所有朋友的友好度之和,对 998244353 取模的结果。
现在,白浅妹妹数出了每一位同学的存在感,但她却不小心忘记了他们友好度。 白浅妹妹想知道,对于给出的存在感,能否还原出所有同学的友好度呢?
大样例: example.zip
输入
第一行输入两个正整数 n, k 。
第二行有 (k + 1)n 个自然数, 按 k + 1 进制下从小到大的顺序,表示每一个人的存在感。
输出
先输出一个数字 k ,表示能否进行还原。
若 k = 0 ,表示不存在任何一组合法的友好度;
若 k = 1 ,表示至少存在一组合法的友好度;
若 k ≠ 0 ,在第二行输出任何一组合法的友好度,顺序与输入相同。 你需要保证输出的数字为 [0,998244353) 间的自然数。
样例输入 复制
1 4
0 1 2 5 4样例输出 复制
1
3 998244350 1 4 0提示
【样例 1 输入】
1 4
0 1 2 5 4
【样例 1 输出】
1
3 998244350 1 4 0
【说明】
这个样例在模意义下仍然存在多解。
例如 2 998244351 1 3 1 仍然为一组合法的输出。
【样例 2 输入】
1 6
0 1 2 2 2 1 1
【样例 2 输出】
1
0 0 1 1 0 1 0
【说明】
这是唯一的解
【样例 3 输入】
1 4
0 1 2 5 3
【样例 3 输出】
0
【备注】
对于所有数据,保证: 1 ≤ n ≤ 10^6
0 ≤ k ≤ 10^6
(k + 1)n ≤ 10^6
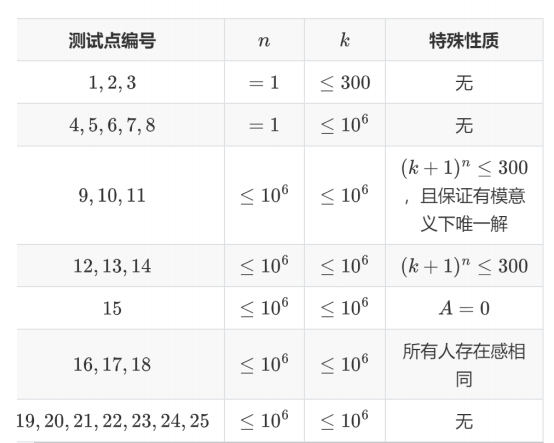
设 A 表示输入友好度的最大值,则 A < 998244353 本题共 25 个测试点,每个测试点 4 分。