4183: 最多可能有多少人开心
内存限制:1024 MB
时间限制:2.000 S
评测方式:文本比较
命题人:
提交:1
解决:1
题目描述
## 输入格式
输入从标准输入中给出,格式如下:
$N$
$p_0$ $p_1$ $\cdots$. $p_{N-1}$
输入
## 输入格式
输入从标准输入中给出,格式如下:
$N$
$p_0$ $p_1$ $\cdots$. $p_{N-1}$
输出
## 输出格式
输出所求答案。
样例输入 复制
4
1 2 0 3样例输出 复制
4提示
## 输入输出样例
### 输入样例1
```
4
1 2 0 3
```
### 输出样例1
```
4
```
### 输入样例2
```
3
0 1 2
```
### 输出样例2
```
3
```
### 输入样例3
```
10
3 9 6 1 7 2 8 0 5 4
```
### 输出样例3
```
5
```
## 数据范围与提示
【样例1说明】
下图显示了执行一次操作后的桌子状态。
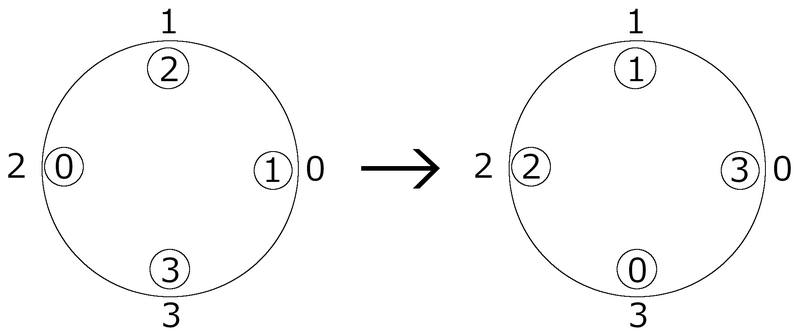
此时有四个人感到高兴:
- 第 0 个人高兴,因为 0 号盘子在第 3 个人(= (0-1) mod 4)面前;
- 第 1 个人高兴,因为 1 号盘子在第 1 个人(= 1)面前;
- 第 2 个人高兴,因为 2 号盘子在第 2 个人(= 2)面前;
- 第 3 个人高兴,因为 3 号盘子在第 0 个人(= (3+1) mod 4)面前。
不可能有 5 个或更多的人感到高兴,所以答案是 4。
【数据范围】
- $3 \leq N \leq 2 \times 10^5$
- $ 0 \leq p_i \leq N-1$
- 如果 $i \neq j$,则 $p_i \neq p_j$
- 所有输入均为整数。
## 题目来源
ABC268C